Table of Contents
Guide To Find Length of the Arc of the Parabola: In mathematics, a parabola is said to be a plan curve and it is mirror-symmetrical, which is U-shaped approximately. One description for parabola involves a point & line, and the focus does not lie on the directrix.
Parabola is defined as a special curve, which is shaped like an arc and is considered as the type of conic section. The symmetrical curve is created by the intersection of a right circular cone along with a surface and this U-shaped curve comes with specific properties.
You can say that it can be concluded at any point on the curve but at an equal distance. The calculation for a parabola is tricky so, you can account for an online parabola calculator that allows you to determine the standard form and vertex form depending on the parabola equation for the given values.
Length of an Arc of Parabola:
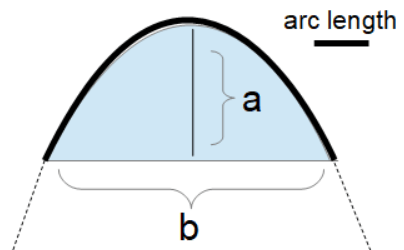
The arc length of the parabola is said to be the distance between two points having a section of a curve. Calculating the length of an irregular arc segment is known as the rectification of a curve.
The advent of the infinitesimal calculation leads to the general formula, which gives closed-form solutions in few cases. The points on the arc curve are difficult to calculate but the directrix of the parabola becomes easy by using the parabola equation calculator.
Parabola Formula:
The simplest form of parabola formula looks like this: y = x 2
In general, the formula is y2 = 4ax
You can use these formulas to find the length of the arc parabola for the manual calculation. But calculating the length by hand might be complex for you, so you can use the parabola calculator to find the length easily.
Read Also: Top 10 useful calculators for students in 2021
Finding the Length of the Arc of the parabola Manually:
Usually, definite integrals are used to find the arc length of a curve. Let’s say that the arc length is the distance you would travel if you are walking along the path of the parabola curve. There are so many real-world examples in which arc length is involved.
Let’s suppose that a rocket is launched along the parabola path, and then we might want to calculate how far the rocket travels. Or if a curve on the map represents a road then, we might want to determine how far we have to travel to reach the destination.
We first need to calculate the arc length of the curve, which is defined as a function of xx, and then we examine this process again for the curves that are defined by the functions of yy.
Here, the technique that is used to find the arc length can be extended to determine the surface area of the surface revolution, and after that, we close the section with an examination of this concept.
The whole procedure of finding the length for the arc of the parabola is tricky when we do it by ourselves. However, we can calculate the length for the arc of the parabola by utilizing the parabola calculator that can generate instant results according to the parabola formula.
Read Also: List of 15 useful health-related calculators
Conclusion:
In this article, the mainly discussed topic is to find the length of the arc of the parabola. Usually, there are two procedures used to find the arc length, one of them is using the parabolic formula, and the other one is using the integral functions in the manual calculations.
The arc length for the parabola is calculated by determining the distance between the two points and the irregular arc segment length is often called rectification of a curve.
Calculating the length on a paper might be critical and complex, so you can consider the parabola calculators like symbolab, easycalculation, emathhelp, and omnicalculator, when you need to find the length as quickly as possible.
Read Also: Percentage calculator is a must online tool for math students
